Optical Rays

Optical rays are the single line or narrow beam of light from a small or distant source.

The behavior of light is easier some time by using ray tracings than by using the EMT. For behaviors of light some time photon theory is also used.

The EMT is used when there is discussion of wavelength and frequency. Using optical rays the explanation of reflection and refraction are much easier propagation of light in fiber also explained in terms of rays. The photon theory is used largely in explaining and analyzing the light generation and detection.

Reflection

The phenomenon related to the bouncing back of light at boundary of two media is called reflection.

Or

When light beam is incident of opaque polished surface than it is returned in general direction of incident light. This returning in general direction of incident light is called reflection.

Its best example is reflection from mirror.

Law of reflection

This law states that “the angle of incidence is equal to the angle of reflection”

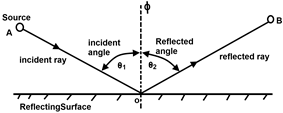
Here the incident ray is line AO, reflected ray is OB and perpendicular to the reflecting surface is ɸ. The incident angle is θ1 and reflected angle is θ₂. Each θ₁ and θ₂ is between ray and perpendicular line to surface.

θ₁ = θ₂

The Fermat’s principle is that “the ray will travel a path, requiring the least amount of time” a direct result of this law is the fact that if θ1 is 90^o, θ₂ is 90^o then reflected ray is in line with the incident ray,

By using this principle we can easily derive the law of reflection and also of refraction.

Refraction

The phenomenon related to the bending of light when it passes or enters from one medium to another is called refraction.

When a ray travels across a boundary between two materials with different refractive indexes n₁ and n₂, so both the refraction and reflection takes place, as shown below

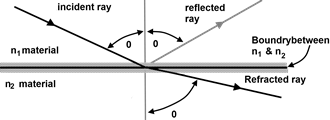
Clearly the shown figure reveals that n₁ > n₂, where the light travels from high to low refractive index materials and so bends away from normal.

In figure θ₁ = θ₂ (As law of reflection)

The refracted ray is that ray which is continuous in the same basic direction as incident ray but slightly bended/braked. So the θ₁ is not equal to θ₃

i.e,   θ₁ + θ₃

Snell’s Law of reflection

The Snell law of refraction gives the important reflection between θ₁ and θ₃ (of fig 3). i.e. incident ray angle & refracted ray angle. Mathematical form of Snell law is

n₁ sinθ₁ = n2 sinθ₂

sinθ₁ / sinθ₂ = n₂/n₁ --------------- (1)

So Snell law states that a ray traveling from high to low index material will more away from perpendicular therefore the angle of incident ray is smaller than that refracted ray similarly if a ray traveling from low to high index material than it move toward the perpendicular and so the angle of incident ray is larger than that of reflected ray

In terms of propagation velocities in the media the reaction between incident and reflected angles is

sinθ₁ / sinθ₂ =V₁ / V₂

Remember that the two materials involved are transparent and allow light propagation.

Note: when both reflection take place than the amount of light reflective depends on the angle of incident angle (similar than about 30^o) the reflected light amount is less than 5% of incident light amount.

An estimate of fraction of light energy that is reflected for a 0 incident angle is

P = ((n₁ – n₂) / (n₁ + n₂))²       (It is power loss)

Total Internal Reflection

 When a ray incident on the interface between high and low reflective index materials is totally reflected rather than refracted than it is called total internal reflection.

Let us taking a particular condition that when angle of reflection say θ₂ is equal to 90 than the refracted beam is not traveling though the n₂ material shown as

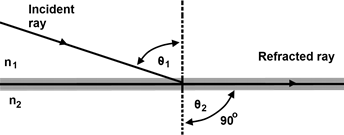
Using Snell’s law we have

Now this angle of incident θ₁ for which refracted angle θ2 = 90^o is called the critical angle θ_c. Thus (1) can be written as

θ₁=θ_c= sin^-1 ( n₁/n₂).

Since n₂<n₁ so the fraction =  is less than 1 and therefore θ_c (critical angle) is less than 90.

Therefore no refraction rays for the case where θi ≥ θc means that incident light is reflected when the incident angle is larger than critical angle (θ_c).This condition is called total internal refraction which can occur only when light travels from high refractive index material to low refractive index material.

Diffraction

The process that causes an electromagnetic wave to bend as it passes by a sharp edge (edge of razor blade) obstructing the wave is called diffraction.

Simply we can say that diffraction causes the light ray to deviate from a straight line. This occurs only when a light wave front is blocked by sharp edge of the object.

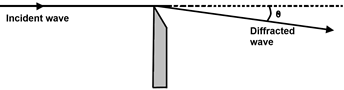
The θ which is the angle of diffraction depends on the wave length λ of the incident light. The result of this relationship between θ and λ is that the diffracted light is dispersed much like light refracted through a prism, giving rise to the rainbow effect as shown in figure.

The diffraction also takes place when a light passes through a narrow slit or a small hole (relative to wavelength) with well defined edges. The diffraction through slits is used in constructing diffraction grating to obtain more efficient diffraction.

Diffraction grating

It is a set of opaque or reflective slits (about the size of λ) spaced at constant distance (S), shown as:

The above shown figure is simple version of diffraction grating. The distance between slits is “S” and is constant over whole plate. The “S” is of the order of magnitude of λ. So the light passes through the slits and is directed.

These are two types of the diffraction grating

1. Transmissive

2. Reflective

Transmissive diffraction grating is constructed by scribing thin lines in a dark film coating that covers the transparent material. This process yields a plate with alternating opaque & transparent slits.

Reflective diffraction grating is the slits in above figure are actually reflecting surfaces. The cumulative affect of reflection from all the reflective strips results in a diffracted wave front that travels in general direction back to light source.

The law governing the transmissive diffraction grating can be states as:

“When a monochromatic light (means light of single λ) is incident on the grating at angle θi, than may diffracted wave are produced. The wave proceeding in the direction of incident light is called zero order wave. The other waves of different order (1^st, 2^nd,3^rd etc) are directed at different angles by diagram we have.

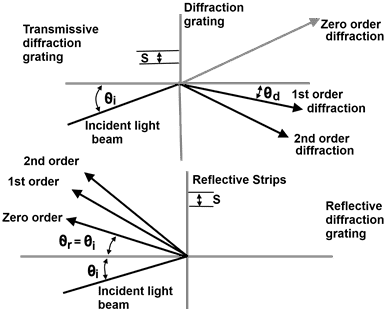
The figure shows light diffraction by diffraction grating.

Now relationship between wave length(λ), diffraction spacing (means distance between slits (S), angle of incidence (θ_i) and angle of diffraction (θ_d)is:

m X (λ/S) = Sinθ_i + Sinθ_d

Where m = ±1, ±2 …..

if m = -1, than

λ /S = Sinθ_i + Sinθ_d

Sinθ_d = (λ/S) – Sinθ_i

θd = Sin^-1((λ/S) – Sinθ_i)

Required equation for diffraction angle.