Phase Modulation - PM
Phase Modulation (PM) is another form of angle modulation. PM and FM are closely related to each other. In both the cases, the total phase angle θ of the modulated signal varies. In an FM wave, the total phase changes due to the change in the frequency of the carrier corresponding to the changes in the modulating amplitude.
In PM, the total phase of the modulated carrier changes due to the changes in the instantaneous phase of the carrier keeping the frequency of the carrier signal constant. These two types of modulation schemes come under the category of angle modulation. However, PM is not as extensively used as FM.
Definition and Physical Appearance of PM
Phase modulation is defined as the process in which the instantaneous phase of the carrier signal is varied in accordance with the instantaneous amplitude of the modulating signal. In this type of modulation, the amplitude and frequency of the carrier signal remains unaltered after PM. The modulating, signal is mapped to the carrier signal in the form of variations in the instantaneous phase of the carrier signal.
The physical appearance of a PM signal for a sinusoidal modulating signal cannot be illustrated because it is impossible to show the phase changes in the modulated earlier at each instant of time. Therefore, a square wave is used as the modulating signal to show the phase change of the modulated carrier with the change in the modulating amplitude. Figure (a) illustrates the modulated carrier signal for a non-sinusoidal, square wave-modulating signal, in this modulating, signal changes its amplitudes at time instances, t1,t2,t3,t4 and t5. According to the definition of PM, the phase of the carrier changes in proportion to the variation in the modulating amplitude at these time instants. in Figure (a), before t1, between time zero and t1, the modulating amplitude is zero. Therefore, during this period, there is no modulation in the Carrier signal and the phase remains unchanged. The same thing happens alter time t5, as the modulating amplitude becomes Zero.
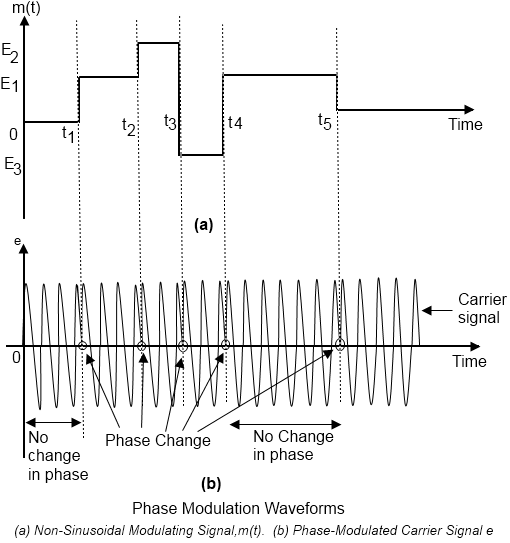
At time t1, the amplitude of m(t) increases from zero to E1. Therefore, at t1, the phase modulated carrier also changes corresponding to E1, as shown in Figure (a). This phase remains to this attained value until time t2, as between t1 and t2, the amplitude of m(t) remains constant at El. At t2, the amplitude of m(t) shoots up to E2, and therefore the phase of the carrier again increases corresponding to the increase in m(t). This new value of the phase attained at time t2remains constant up to time t3. At time t3, m(t) goes negative and its amplitude becomes E3. Consequently, the phase of the carrier also changes and it decreases from the previous value attained at t2. The decrease in phase corresponds to the decrease in amplitude of m(t). The phase of the carrier remains constant during the time interval between t3 and t4. At t4, m(t) goes positive to reach the amplitude El resulting in a corresponding increase in the phase of modulated carrier at time t4. Between t4 and t5, the phase remains constant. At t5 it decreases to the phase of the unmodulated carrier, as the amplitude of m(t) is zero beyond t5.
Equation of a PM Wave
To derive the equation of a PM wave, it is convenient to consider the modulating signal as a pure sinusoidal wave. The carrier signal is always a high frequency sinusoidal wave. Consider the modulating signal, em and the carrier signal ec, as given by, equation 1 and 2, respectively.
em = Em cos ωm t ------------(1)
ec = Ec sin ωc t ---------------(2)
The initial phases of the modulating signal and the carrier signal are ignored in Equations (1) and (2) because they do not contribute to the modulation process due to their constant values. After PM, the phase of the carrier will not remain constant. It will vary according to the modulating signal em maintaining the amplitude and frequency as constants. Suppose, after PM, the equation of the carrier is represented as:
e = Ec Sin θ ------------------(3)
Where θ, is the instantaneous phase of the modulated carrier, and sinusoid ally varies in proportion to the modulating signal. Therefore, after PM, the instantaneous phase of the modulated carrier can be written as:
θ = ωc t + Kp em -------------------(4)
Where, kp is the constant of proportionality for phase modulation.
Substituting Equation (1) in Equation (4), yon get:
θ = ωc t + Kp Em Cos ωm t ---------------------(5)
In Equation (5), the factor, kpEm is defined as the modulation index, and is given as:
mp = Kp Em ------------------------(6)
where, the subscript p signifies; that mp is the modulation index of the PM wave. Therefore, equation (5) becomes
θ = ωc t + mp Cos ωm t ---------------------(7)
Substituting Equation (7) and (3), you get:
e = Ec sin (ωct + mp cos ωmt) --------------------(8)
Equation (8) is the final expression of the PM wave.
