Terms Of Modulation
Modulation index
"The ratio of the frequency deviation to the modulating frequency is known as the modulation index."
Symbolized by m
M = fd/fm (in radians)
Where
fd = frequency deviation
fm = modulating frequency
For example, assume that the maximum frequency deviation of the carrier is ± 25 KHz while the maximum modulating frequency is 10 KHz. The modulation index, therefore, is
mf = 25/10 = 2.5 rad
Note
The modulation index can originally know as the modulation factor; hence the symbol mf.
Note
The modulation index is a measure of radian phase shift of the modulated FM signal compared to the phase of the un-modulated carrier alone.
In most communications systems using FM, maximum limits are put on both the frequency deviation and modulating frequency. For example, in standard FM broadcasting, the maximum permitted frequency deviation is 75 KHz, while the maximum permitted modulating frequency is 15 KHz. This produces a modulation index ofmf = 75/15 = 5 rad.
Whenever the maximum allowable frequency deviation and the maximum modulating frequency are used in computing the modulation index, mf is known as the deviation ratio.
The audio broadcast in T.V. is transmitted by FM. The maximum deviation permitted is 25 KHz and the maximum modulating frequency is 15 KHz. This produces a deviation ratio of
d = 25/15 = 1.67 rad
In standard two-way mobile radio communications using FM, the maximum permitted deviation is usually 5 KHz. The upper modulating frequency is usually limited to 2.5 KHz which is high enough for intelligible voice transmission. This produces a deviation ratio of
d = 5/2.5 = 2 rad
Percentage of Modulation
The maximum deviation permitted can be used in a radio with the actual carrier deviation to produce a percentage of modulation for FM. Remember, in commercial FM broadcasting the maximum allowed deviation is 75 KHz. If the modulating signal is producing only a maximum deviation of 60 KHz, then the FM percentage of modulation is
FM percent modulation
= (Actual carrier deviation/Maximum carrier deviation) * 100
= (60/75) x 100
= 80%
Frequency Deviation
The change in carrier frequency is called the frequency deviation." and uses symbol ∆fc (∆ is the Greek letter delta and is used to symbolize change). For a sample transmitter with an assigned rest frequency of 100MHzdeviated by ±25KHz, The carrier change frequency with modulation between the limits of 99.975 .MHz and 100.025 MHz The total frequency change of 2 x 25 KHz = 50 KHz is called the carrier swing.
Frequency Swing
"Frequency swing is the total deviation above and below the center frequency."
It is the total frequency change above and below the center frequency. In above example, frequency swing is 50 KHz. It is also called the carrier swing.
Effective side band, Bandwidth
Bassel function Graph
Figure shows an example of the spectrum of a typical FM signal produced by modulating a carrier with a single-frequency sine wave. Note that the sidebands are spaced from the carrier fc and are spaced from one another by a frequency equal to the modulating frequency fm. If the modulating frequency is 500Hz, the first pair of side-bands is above and below the carrier by 500Hz. The second pair, of side-bands is above and below the carrier by 2 x 500 Hz = 1000 Hz, or 1 KHz, and so on.
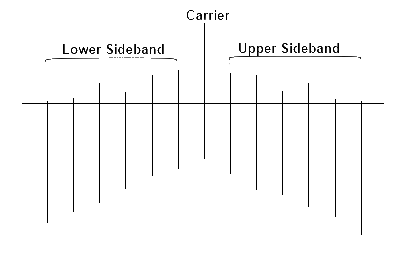
As the amplitude of the modulating signal varies, of course, the frequency deviation will change. The number of side-bands produced, their amplitude, and their spacing depend upon the frequency deviation and modulating, frequency. Keep in mind that an FM signal has constant amplitude. If that FM signal is a summation of the side-band frequencies, then can see that the sideband amplitudes must vary with frequency deviation and modulating frequency if their sum is to produce fixed amplitude FM signal.
Although the FM process produces an infinite number of upper and lower side-bands, only those with the largest amplitudes are significant in carrying the information which are also called effective side-bands. Typically any side-band whose amplitude is less than 1 percent of the un-modulated carrier is considered insignificant. As a result, this markedly narrows the bandwidth of an FM signal. Due to which its bandwidth is narrow.
| Modulation Index | Sidebands (Pairs) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Carrier | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th | 9th | 10th | 11th | 12th | 13th | 14th | 15th | 16th | |
| 0.00 | 1.00 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 0.25 | 0.98 | 0.12 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 0.5 | 0.94 | 0.24 | 0.03 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 1.0 | 0.77 | 0.44 | 0.11 | 0.02 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 1.5 | 0.51 | 0.56 | 0.23 | 0.06 | 0.01 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 2.0 | 0.22 | 0.58 | 0.35 | 0.13 | 0.03 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 2.5 | -0.06 | 0.50 | 0.45 | 0.22 | 0.07 | 0.02 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 3.0 | -0.20 | 0.34 | 0.49 | 0.31 | 0.13 | 0.04 | 0.01 | -- | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 4.0 | -0.40 | -0.07 | 0.36 | 0.43 | 0.28 | 0.13 | 0.05 | 0.02 | -- | -- | -- | -- | -- | -- | -- | -- | -- |
| 5.0 | -0.18 | -0.33 | 0.06 | 0.36 | 0.39 | 0.26 | 0.13 | 0.05 | 0.02 | -- | -- | -- | -- | -- | -- | -- | -- |
| 6.0 | 0.15 | -0.28 | -0.24 | 0.11 | 0.36 | 0.36 | 0.25 | 0.13 | 0.06 | 0.02 | -- | -- | -- | -- | -- | -- | -- |
| 7.0 | 0.30 | 0.00 | -0.30 | -0.17 | 0.16 | 0.35 | 0.34 | 0.23 | 0.13 | 0.08 | 0.02 | -- | -- | -- | -- | -- | -- |
| 8.0 | 0.17 | 0.23 | -0.11 | -0.29 | -0.10 | 0.19 | 0.34 | 0.32 | 0.22 | 0.13 | 0.06 | 0 | -- | -- | -- | -- | -- |
| 9.0 | -0.09 | 0.24 | 0.14 | -0.18 | -0.27 | -0.06 | 0.20 | 0.33 | 0.30 | 0.21 | 0.12 | 0.1 | 0.03 | 0.01 | -- | -- | -- |
| 10.0 | -0.25 | 0.04 | 0.25 | 0.06 | -0.22 | -0.23 | -0.01 | 0.22 | 0.31 | 0.29 | 0.20 | 0.1 | 0.06 | 0.03 | 0.01 | -- | -- |
| 12.0 | -0.05 | -0.22 | -0.08 | 0.20 | 0.18 | -0.07 | -0.24 | -0.17 | 0.05 | 0.23 | 0.30 | 0.3 | 0.20 | 0.12 | 0.07 | 0.03 | 0.01 |
| 15.0 | -0.01 | 0.21 | 0.04 | 0.19 | -0.12 | 0.13 | 0.21 | 0.03 | -0.17 | -0.22 | -0.09 | 0.10 | 0.24 | 0.20 | 0.25 | 0.18 | 0.12 |
Knowing the modulation index, you can compute the number and amplitudes of the significant side-bands. This is done through a complex mathematical process known as the Bassel functions. The typical Bassel function graph is shown in the table. The left hand column gives the modulation index. The remaining columns indicate the relative amplitudes of the carrier and the various pairs of side-bands. Any side-bands with a relative carrier amplitude' of less than 1 percent (0.01) has been eliminated.
The total bandwidth of an FM signal can be determined by knowing the modulation index and using the table. For example, assume the modulation index is 2. Referring to the table, you can see that this produces four significant pairs of side-bands. The bandwidth can then be determined with the simple formulae.
BW = 2fm x number of significant side-bands.
Using the example above and assuming a highest modulating frequency of 2.5 KHz, the bandwidth of the FM signal is
BW = 2 (2.5) (4) = 20 KHz
An FM signal with a modulation index of 2 and a highest modulating frequency of 2.5 KHz will then occupy a bandwidth of 20 KHz.
