Faraday's law's of Electromagnetic induction

In 1831, the brilliant scientist Michael Faraday unveiled a groundbreaking phenomenon known as electromagnetic induction, forever altering our understanding of the relationship between electricity and magnetism. 

This ingenious process, which he meticulously experimented with, involves generating an electric current through the manipulation of magnetic flux.

Faraday's initial exploration of electromagnetic induction involved an iron ring upon which he wound two separate coils. Upon closing a switch connected to the system, he observed a remarkable result: a noticeable deflection on a galvanometer, an instrument used to detect and measure electric currents. 

However, the real marvel lay in what occurred when the switch was opened - the galvanometer's deflection was now in the opposite direction. This intriguing observation provided a clue into the transformative power of electromagnetic induction.

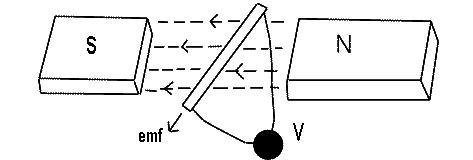
Further experimentation by Faraday involved moving a permanent magnet towards and away from a coil. Astonishingly, he witnessed a similar deflection in the galvanometer. This uncanny similarity led Faraday to a profound conclusion: the movement of magnetic flux relative to a coil could induce the generation of an electric current. This revelation marked a fundamental shift in our comprehension of the interplay between electricity and magnetism.

Faraday's insights also extended to quantifying this induced effect. He determined that the magnitude of the induced electromotive force (e.m.f.), which drives the flow of electric current, is directly proportional to the rate at which the magnetic flux passing through the coil changes. In simpler terms, the faster the magnetic flux is altered, the stronger the induced e.m.f. becomes. This elegant relationship became a cornerstone of electromagnetic theory.

An alternative perspective on this phenomenon emerged: as a conductor interacts with magnetic flux by either cutting through it or being cut by it, an electromotive force is generated in the conductor. This induced e.m.f. is directly proportional to the rate at which the conductor's interaction with the magnetic flux changes. This principle effectively bridged the gap between magnetism and electricity, laying the foundation for a multitude of technological advancements.

In summary, Michael Faraday's groundbreaking work on electromagnetic induction unveiled a remarkable connection between electricity and magnetism. His experiments with coils, switches, and magnets illuminated the concept that the movement of magnetic flux relative to a conductor could create an electric current. 

The induced electromotive force's strength depended on the rate of change of magnetic flux, ultimately leading to the birth of a transformative scientific principle that continues to shape the world of physics and engineering.

Faraday's First Law of Electromagnetic Induction:

"A change in the magnetic field within a closed loop of wire induces an electromotive force (emf) in the loop, causing an electric current to flow if the circuit is closed."

This law is a fundamental principle that highlights the essential connection between changing magnetic fields and the generation of electric currents. Let's break down the components of this law:

1. Change in Magnetic Field: Whenever there is a change in the strength of a magnetic field, such as an increase or decrease, or a change in the orientation of magnetic field lines within a region, this change induces a response in the surrounding environment.
2. Closed Loop of Wire (Circuit): To harness the induced emf and create an electric current, the wire must form a closed loop or circuit. This means that the wire creates a continuous path for the electric charges (usually electrons) to flow.
3. Electromotive Force (emf): As previously mentioned, emf is a potential difference or voltage. In this context, it refers to the voltage induced in the closed loop of the wire due to the changing magnetic field. This induced emf drives the flow of electric charges within the circuit.

Faraday's first law captures the core principle of electromagnetic induction: a changing magnetic field induces an emf in a closed loop of wire. This emf, in turn, generates an electric current in the circuit if it is closed. It's important to note that the induced current only flows while there is a change in the magnetic field; once the field stabilizes, the induced current decreases and eventually stops.

The first law of electromagnetic induction is the foundation upon which Faraday's subsequent laws and the entire field of electromagnetism are built. It forms the basis for various applications, including the generation of electricity in power plants, the operation of electric motors, and the functioning of transformers. Understanding and harnessing the principles of electromagnetic induction have revolutionized technology and enabled the development of numerous devices and systems that power our modern world.

Faraday's Second Law of Electromagnetic Induction:

It seems you're referring to Faraday's second law of electromagnetic induction. Faraday's second law builds upon his initial discovery and provides a deeper understanding of the relationship between magnetic fields, electric currents, and the concept of induction.

"The magnitude of the electromotive force (emf) induced in a closed loop is directly proportional to the rate of change of magnetic flux passing through the loop."

Let's break down this law step by step:

1. Electromotive Force (emf): The electromotive force, often abbreviated as emf, is not an actual force but rather a potential difference or voltage. It represents the driving force that pushes charges (electrons) to move in a closed circuit, creating an electric current.
2. Closed Loop: A closed loop refers to a circuit that forms a complete path for the electric current to flow. It can be a simple loop of wire or a more complex arrangement of conductors.
3. Magnetic Flux: Magnetic flux is a measure of the magnetic field passing through a given area. It depends on the strength of the magnetic field, the angle between the magnetic field lines and the surface area, and the orientation of the area with respect to the magnetic field.
4. Rate of Change: This refers to how quickly the magnetic flux passing through the closed loop changes. It could change because the magnetic field strength changes, the loop moves within the magnetic field, or the angle between the loop and the magnetic field changes.

Faraday's second law essentially states that if you have a closed loop of wire (a circuit), any change in the magnetic flux passing through that loop will induce an emf in the loop. The magnitude of this induced emf is directly proportional to the rate at which the magnetic flux changes.

Mathematically, Faraday's second law can be expressed as:

emf = -N * d(Φ) / dt

Where:

• emf is the induced electromotive force (voltage).
• N is the number of turns (loops) in the wire.
• d(Φ) / dt is the rate of change of magnetic flux through the loop.

The negative sign indicates that the direction of the induced current opposes the change in magnetic flux (Lenz's law), which is a crucial aspect of electromagnetic induction.

In practical terms, Faraday's second law is fundamental in various applications, from power generation in electric generators to the functioning of transformers and many other electromagnetic devices. It's a cornerstone of electromagnetism and has paved the way for numerous technological advancements.

FARADAY'S LAW'S EXPLANATION

Let

Initial flux linkages = Nφ1

Final flux linkages = Nφ2

Change in flux linkages= Nφ2 – Nφ1

= N((φ2-φ1)

If (φ2-φ1) = φ

Then change in flux linkages = Nφ

Rate of change of flux linkages = Nφ/t wb/sec

Taking the derivative of the right-hand side we get

Rate of change of flux linkages = Ndφ/dt wb/sec

But according to Faraday's laws of electromagnetic induction, the rate of change of flux linkages is equal to the induced emf, hence we can write

= Ndφ/dt volt

Generally, Faraday's laws are written as

e = -Ndφ/dt volt

Where the negative sign represents the direction of the induced current in the conductor will be such that the magnetic field produced by it will oppose the verb cause to produce it.