Kirchhoff's Current Law (KCL)
Kirchhoff's current law is stated as follow,
The sum of the current into a junction is equal to the sum of the current out of at junction.
A junction is any point in a circuit where two or more circuit paths comes together. In parallel circuit, a junction is a point where the parallel branches connect together. The following is another way to state Kirchhoff's current law:
The total current into a junction is equal to e total current out of that junction.
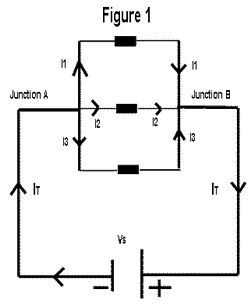
For example, in the circuit of figure 1, point A is one junction and point B is another. Let us start at the negative terminal of the source and follow the current. The total current IT flows from the source and into the junction at point A. At this point, the current splits up among the three branches as dictated. Each of three branch current (I1, 12, and I3) flows out of the junction A. Kirchhoff's current law says that the total current into junction A is equal to the total current out of junction A; that is
IT = I1 + I2 + I3
Now, they come back together at point B.
Currents I1, I2 and I3 flow into junction B, and IT flows out. This junction is therefore the same as at junction A
I1 + I2 + I3 = IT
Kirchhoff's current law is sometimes stated in this way:
The algebraic sum of all the currents entering and leaving a junction is equal to zero.
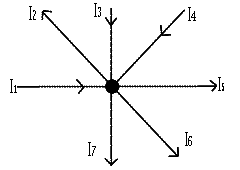
KCL ( Kirchhoff Current Law ) EQUATION
In the given fig I1, I2, I3, I4, I5, I6, I7 are different currents in which some current leaving the point (A) and some current meeting at point (A). We taking the incoming current as positive and out going current as negative according to KCL ( Kirchhoff Current Law) the equation will be as follow.
I1 + ( -I2 ) + I3 + I4 + ( -I5 ) + ( -I6 ) + ( -I7 ) = 0
I1 - I2 + I3 + I4 - I5 - I6 - I7 = 0 —>(1)
This is called KCL ( Kirchhoff's Current Law ) equation
I1 + I3 + I4 = I2 + I5 + I6 + I7 —>(2)
From equation (2) it is clear that sum of currents flowing towards point (A) is equal to the sum of current flowing away from it.
