Kirchhoff's Voltage Law (KVL)

Kirchhoff Voltage Law states that ''The algebraic sum of all voltages (source voltage and voltage drops) is equal to zero around a close path''.

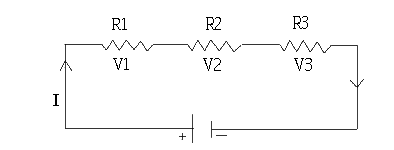
In the above circuit R₁, R₂ and R₃ are three resistors connected in series across a voltage source V. V_I , V₂ and V₃ are voltage drops across resistors R₁, R₂ and R₃ respectively. So according to Kirchhoff voltage law

V + ( -V₁ ) + ( -V₂ ) + ( -V₃ ) = 0

V - V₁ - V₂ - V₃ = 0

V = V_I + V₂ + V₃

This is called KVL ( Kirchhoff Voltage Law) equation.

V = V_I + V₂ + V₃

Applied voltage = sum of all voltage drops

OR

The source voltage is equal to the sum of all voltage drops.