Mesh Current Method
In the mesh current method, you will work with loop currents instead of branch currents. A branch current is the actual current through a branch. An ammeter placed in a given branch will measure the branch current. Loop currents are different because they are mathematical quantities that are used to make circuit analysis somewhat easier than branch current method. The term mesh comes from the fact that a multiple - loop circuit, when drawn, can be imagined to resemble a wire mesh.
A systematic method of mesh analysis is listed in the following steps and is illustrated in figure.
| Step 1 | Assign a current in the clock wise (CW) directions around each closed loop. This may not be the actual current direction. |
| Step 2 | Indicate the voltage drop polarities in each loop based on the assigned current direction. |
| Step 3 | Apply Kirchhoff s voltage law around each closed loop. When more than one loop current passes through a component; include its voltage drop. This results in one equation for each loop. |
| Step 4 | Using substitution, solve the resulting equations for the loop currents. |
CIRCUIT FOR DEMONSTRATING MESH ANALYSIS
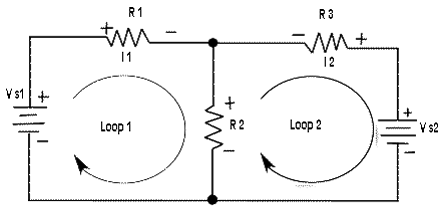
| First | The loop currents I1 and I2 are assigned in the CW direction as shown in the figure. |
| Second | The Polarities of the voltage drops across R1, R2 and R3 are shown based on the loop current directions. Notice that I1 and I2 flow in Opposite directions through R2 because R2 is common to both loop Therefore, two voltage polarities are indicated. In reality, R2 currents can be separated into two parts, but remember that the loop currents are basic mathematical quantities used for analysis purposes. The polarities of voltage sources are fixed and are not affected by the current assignments. |
| Third | Kirchhoff's voltage law applied to the loops results in the following two equations R1I1 + R2(I1 — I2) = VS1 --------------->for loop l |
| Fourth | The like terms in the equations are combined and rearranged for convenient solution so that they have the same position in each equation, that is, the I1 to is first and the I2 term is second. The equations are rearranged into the following form. Once the loop currents are evaluated, all of the branch currents can be determined. (R1 + R2) I1 - R2I2= VS1 ----------------->for loop 1 |
The format for setting up the equation for a loop circuit can be stated as follows.
- Sum the resistances around the loop, and multiply by the loop current.
- Subtract the common resistance times the adjacent loop current sign of the sourco voltage.
- Set the terms in steps 1 and 2 equal to the total source voltage in the loop is positive! the assigned loop current flows out of its positive terminal. the sign is negative if the loop current flows into its positive terminal.
- Rearranee the terms so that like terms appear in the same position in each equation.
EXAMPLE
Illustrates the application of this format to the mesh current analysis of a circuit shown in figure-1
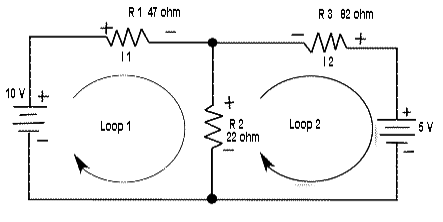
SOLUTION
Assign the loop currents as shown in figure-1. Use the format describe to set up the two loop equations.
(47 + 22)I1 — 22I2 = 10 --------->for loop 1
69I1 — 2212 = 10------------------------> (1)
—22I1 + (22 + 82)I2 = —5 ----------------->for loop 2
— 22I2 + 104I2 = —5 --------------------> (2)
From (2)
I2 = (22I1 - 5)/104
Put in (1)
69I1 — 22((22I1 — 5)/104) = 10
7176I1 — 484I1 + 110 = 1040
6692I1 = 930
| I1 = 0.139 Ampere |
I1 = 139mA
Put in (1)
69(0.139) - 22I2 = 10
9.591 - 22I2 = 10
22I2 = 9.591 - 10
22I2 = - 0.409
| I2 = —0.0186 Ampere |
I2 = -18.6mA
The negative sing on I2 means that its direction must be reversed.
Now find the actual branch currents. Since I1 is the only current through R1, It is the only branch current IR1,
IR1 = I1 = 139mA
Since I2 is the only current through R3 it is also the branch current IR3 = I2 = -18.6 mA (opposite direction of the originally assigned to I2) Both loop currents I1 and I2 flow through R2 in the same direction.
Remember, The negative I2 value told us to reverse its assigned direction.
IR2 = I1 — I2 = 139mA — (-18.7mA) = 158mA
Keep in mind that once we know the branch currents, we can find the voltages using Ohm's law.
