Hybrid Equivalent of Transistor

Figure(a) shows a transistor amplifier circuit. Such circuit can be connected in any one of the three configuration called common emitter, common base or common collector to a voltage source (V_s) and load resistance (r_i). The voltages source has an internal resistance (R_s) as shown in figure. The load resistance (r_L)) is the effective or A.C load resistance seen by the transistor at its output. Figure (a) shows the hybrid formulas for input resistance, output resistance, current gain and voltage gain of a transistor.

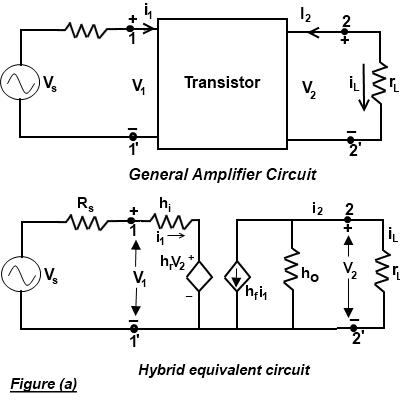
The expression for transistor amplifier input and output resistances, voltage and current gains may be obtained from the relations:

V_i = h₁.i₁ + h_r.V₂ ---------------(1)
i₂ = h_f.i₁ + h_o.V₂  ----------------(2)

The voltage drop across load resistance (r_L) is equal to the voltage across the output terminals of atransistor.

V₂ = i_L.r_L = -i₂.r_L    (Since i₂ = -i_L)

Current Gain

It is the ratio of output current (i_L) to input currents (i₁). Mathematically, the current gain,

A_i = i₁/i₁ = i₂/i₁

Putting the value of V₂ (equal to –i₂.r_L) in equation (2)

i₂ = h_f.i₁ + h_o(-i₂.r_L) = h_f.i₁ –h_o.i₂.r_L
i₂ + h_o.i₂.r_L = h_f.i₁
i₂(1 + h_o.r_L) = h_f.i₁
i₂/i₁ = h_f/(1 + h_o.r_L)
A_i = i₂/i₁ = -(h_f/(1 + h_o.r_L)) -------------------(3)

Input Resistance

Input resistance value is given by the ratio of input voltage (V₁) to the input current (i₁).
Mathematically,

R_i = V₁/i₁

Again putting the value of V₂ (equal to –i₂.r_L) in equation (1)

V₁ = h_i.i₁ + h_r(-i₂.r_L)
= h_i.i₁ – h_r.i₂.r_L

Dividing the equation (1) by i₁ on both sides,

V₁/i₁ = (h_i.i₁ – h_r.i₂.r_L)/i₁ =h_i – h_r(i₂/i₁)r_L

Replacing v1/i₁ with R_i and i₂/i₁ by –A_i in the above equation.

R_i = h_i – h_r(-A_i).r_L = h_i + h_r.A_i.r_L --------------(4)

Putting the value of A_i equal to –h_f/(1 + h_o.r_L) from equation (3) in the above expression.

R_i = h_i + h_r (-(h_f/(1 + h_o.r_L)r_L)
= h_i – (h_r.h_f/h_o + (1 / r_L)) ----------------- (5)

Voltage Gain

It is defined as the ratio of output voltage (V₂) to the input voltage (V₁).
Mathematically, the voltage gain,

A_v = V₂/V₁ = -(i₂.r_L/V₁)    (as V₂ = -i₂.r_L)

Putting the value of i₂ (equal to –A_i.i₁) from equation (2) the above expression,

A_v = (A_i.i₁.r_L/V₁) = A_i.r_L(i₁/V₁)

Replacing i₁/V₁ by R_i in the above expression,

A = A_i.r_L/R_i

Putting the value of A_i (equal to –h_f/(1 + h_o.r_L) and R_i (equal to h_i – h_r/h_f(h_o + 1/r_L)) in the above expression and re-arranging,

A_v = - ( h_f.r_L/(h_i + (h_i.h_o – h_r.h_f)r₁))

If we replace (h_i.h_o – h_r.h_f = ∆h) in the above expression then the voltage gain,

A_v = -( h_r.r_L/ (h_i + ∆h.r_L))

Output Resistance

It is obtained by setting the source voltage (V_s) to zero and the load resistance (r_L) to infinity and by driving the output terminals from a source V₂ as shown in below Figure (b).

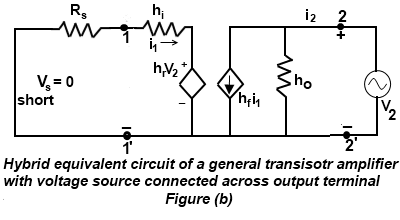
Then output resistance is the ratio of voltage (V₂) to the current drawn from the voltage source (i₂).

Mathematically, the output resistance,

R_o = V₂/i₂ = (V₂/(h_r.i₁ + h_o.V₂) ------------(6)

The value of current (i₁) can be obtained by applying Kirchhoff’s Law to the input side of transistor amplifier circuit.

R_s.i₁ + h_i.i₁ + h_r.V2 = 0
As i₁ = -(h_r.V₂)/ (R_s + h_i)

Putting this value of i₁ in equation (6)

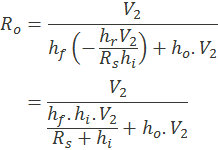
Rearranging the above equation

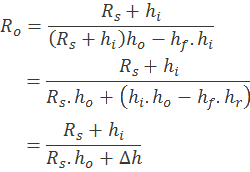
If source resistance (R_s) is zero, then output resistance is,

R_o =  h_i/∆h

Power Gain

It is defined as the product of voltage gain (A_v) and the current gain (∆i).

Mathematically, the power gain is,

∆p = A_v.A_i