Operational Amplifier differentiator & Integrator

Operational Amplifier differentiator

The operational amplifier is an amplifier which is directly coupled between the output and input, having a very high gain. It is used to perform a wide variety of mathematical operations like summation, subtraction, multiplication, differentiation and integration etc. in analogue computers.

An operation amplifier can be used as a differentiator as shown in Fig. 1. This circuit produces an output voltage that is proportional to the time derivative input voltage. Hence this circuit is called differentiator.

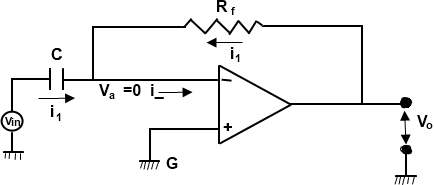
Assuming that G is virtually ground. Since the current flowing in to the virtual ground is equal to current flowing out of it we can write.

i₁= i_f= i_-1
i_ = 0
i₁ = i_f -=0
i₁ = i_f

from the definition of capacitance, the

charge on the capacitor is

q = CV

the charging current i is the time rate of change of charge.

Hence, output voltage V₀ is equal to a constant —RC times the derivative of the input voltage V_i.

Operational Amplifier Integrator

An operational amplifier can also be used as a integrator by changing the position of R and C as shown in Fig. 2. this circuit produces an output voltage that is proportional to the time integral of the input voltage. Hence, this circuit is called an integrator.

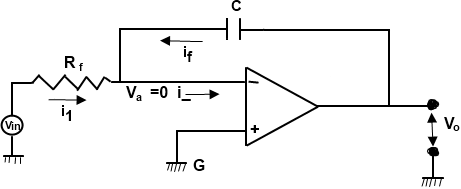
Assuming that G is virtually ground. Since the current flowing in to the virtual ground is equal to the current flowing out of it we can write.

i₁+ i_f  =i_
i_ = 0
i₁+ i_f = 0
i₁ = –i_f

Hence, output voltage V, is equal to a constant -1/RC times the integral of the input voltage V_i.