RC High-Pass Filter Circuit
Fig. 1 shows the series RC high-pass filter circuit. In such circuit, the output is taken across the resistor and practically reactance of the capacitor decrease with increasing frequency. At very high frequencies the capacitor acts as a short circuit and all the input appears at the output. On the other hand, at dc or zero frequency the capacitor has infinite resistance and hence behaves as open circuit, thus blocking the dc voltage. Therefore, capacitor C is called the blocking capacitor.
Sinusoidal Input:
When a sinusoidal input Vi, is applied to it, then the output Vo is given by:
Vo = (R/(R-JXc))Vi
Where
Vo is the output voltage
V2 is the input voltage
Xc is the capacitive reactance
R is the resistance, and
J is the imaginary axis of the complex plane
Output is a frequency dependent quantity. At low frequency, —JXc >>R. Under this condition, expression becomes almost zero i.e.
Vo = 0
At high frequency, —JXc << R. Under this condition, the ratio (R/(R – JXc) becomes unity and Vo = Vi
Thus high-pass circuit attenuates signals of low frequencies and does not affect the high frequency signals. A frequency response curve of a high-pass circuit is shown in Fig. 1(b). The frequency at which the output becomes 70.7 percent of the input is called the lower cutoff frequency and is given by the expression.
fc = 1/2πfc
Step - Voltage Input:
For a step input of Fig. 2(a), the output voltage Vo, which is also voltage across resistor, decay exponentially towards the initial value of V with the time constant RC.
Vo = Ve-1/RC
Effects of the circuits time constant on RC high pass:
The shape of the output waveform of an RC high-pass circuit also depends upon the value of the circuit time constant T. Circuit time constant may be long, short or medium as given by the circuit condition. The output waveforms are the result under these conditions for an RC high-pass are shown in Fig. 3 The output waveform shown in Fig. 3(b) for long time constant is just similar to the input waveform. However, usually a slight tilts exists in it.
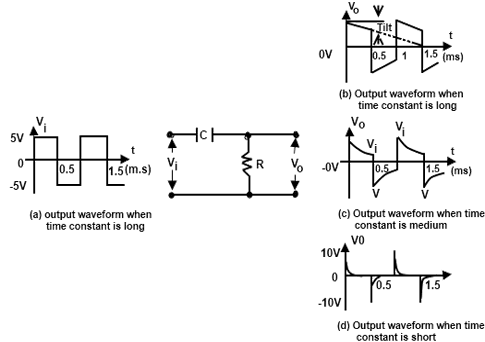
The output waveform under short time constant condition is shown in Fig. 3(d). It consists of positive and negative spikes. This is a differentiated square wave. The RC high-pass circuit under which condition (short time constant) is also known as the differentiator.
High-pass RC circuit as Differentiator:
The High-pass RC circuit is also known as a differentiator. The name high pass is so called because the circuit blocks the low frequencies and allows high frequencies to pass through it. It is due to reason that reactance of the capacitor decreases with the increasing frequency. As a result of this, at very high frequencies, the capacitor acts as a short circuit and virtually all the input appears at the output as explain earlier.
A circuit in which the output voltage is directly proportional to the derivative of the input voltage is called a differentiating circuit. Mathematically, the output voltage is given by:
Output ∝ d/dt (input)
Vo∝ dvi/dt
or Vo= RC d/dt V2
Where RC is a constant of proportionality
A differentiating circuit is a simple RC series circuit with output taken across the resistor R. The circuit is designed in such a way that output is proportional to the derivative of the input. Thus if a d.c. or constant input is applied to such a circuit, the output will be zero. It is because the derivative of the constant is zero.
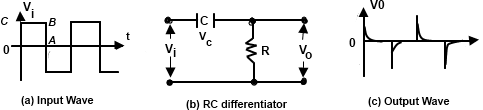
Fig 4 shows a differentiating circuit, the output across R will be derivative of the input. In order to achieve a good differentiation, the following two conditions should be satisfied.
- the time constant RC of the circuit should be smaller than the time period of the input signal.
- the value of a capacitive reactance Xc should be 10 or
more time larger then R at the operating frequency.
Let Vi, be the input alternating voltage and let i be The resulting alternating current. The charge q on the capacitor at any instant is:
q = CVc
i = dq/dt
i = d/dt (CVc)
i = C d/dt (Vc)
Since the capacitive reactance is very larger than R, the input voltage can be consider equal to the capacitor voltage without any error,, i.e Vc = Vi,
i = (C d/dt (Vi))R
output voltage is given by:
Vo = iR
Or Vo =(C d/dt (Vi))R
Vo =RC d/dt Vi
where RC is a constant, and
Hence
Output ∝ d/dt (input)
The output waveform from a differentiating circuit depends upon the time constant and the shape f the input signal. Now let us consider some cases:
Input as a square wave:
When the input applied to a differentiating circuit is a square wave, output will consists of sharp narrow pulses as shown in Fig. 4(c). During the OC part of the input wave, it amplitude changes abruptly and hence the differentiated wave will be sharp narrow pulse. However, during the constant portion CB of the input signal, the output will be zero, because the derivative of a constant is zero.
Inputas a Saw-tooth Wave:
When the input applied to a differentiating circuit is a saw-tooth wave, output will be a rectangular wave as shown in Fig. 5 during the portion OA of the input signal, its amplitude changes at a constant rate and, therefore, the differentiated wave has a constant value for each constant rate of change.
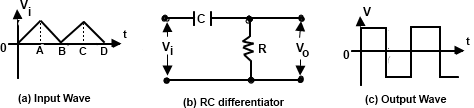
During the portion AB of the input wave, the change is less abrupt so that output will be very narrow pulse of rectangular form. Thus when a sawtooth wave is applied to a differentiating circuit, the output consists of a succession of rectangular wave of equal or unequal duration depending upon the shape of the input signal.
Input as a Triangular Wave:
When the input applied to a differentiating circuit is a triangular wave, output will be a square wave as shown in Fig. 6
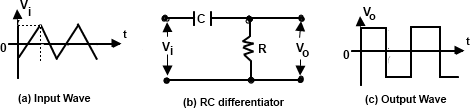
Whenever the slop of the input voltage abruptly changes, the circuit output takes certain finite time to reach to its steady state level. It may be observed that smaller the value of time constant of the differentiating circuit, lesser will be the time taken by its output to reach to its steady state level. However, a smaller time constant reduces the amplitude of the output voltage.
Applications:
Some important applications of a differentiating circuit are given as under:
- To generate a square wave from a triangular wave input.
- To generate a step from a ramp input.
- To generate a series of narrow pulses called spikes from the rectangular or square waveform. The pips are used as trigger pulses or synchronization pulses in circuits used in television and cathode ray oscilloscopes.
