RC Feedback Oscillators
RC oscillators employ resistors and capacitors and are used to generate low or audio-frequency signals. Hence they are also known as audio-frequency (A.F) oscillators. The tuned or LC oscillators are not suitable at low-frequencies because the size of inductors and capacitors becomes very large. In these oscillators the single stage of the amplifier amplifies the input signal and produces a phase shift of 180o. To obtain positive feedback for sustained oscillation, the output of first stage is fed to a phase shift network to produce an additional phase shift of 180°. Thus a total of 360° phase shift which is equivalent to zero occurs. This principle is used in phase shift-oscillators. The most important types of RC feedback oscillators are phase shift and wein bridge oscillators.
Phase Shift Oscillator
Figure shows the circuit of a phase shift oscillator. The feedback network consists of three RC sections. Each section produces a phase shift of 60°. Therefore the net phase shift of the feedback network is 180°, therefore the total phase shift between the input and output circuit is 360° or 0°. The circuit is showing the amplifier and feedback network. The amplifier stage is self-biased with a capacitor by passed emitter resistor RE and collector bias resistor Rc.

When power is applied to the circuit, oscillations are started by any random noise (electrical variations generated internally in components). A change in the flow of base current results in an amplified change in collector current which is in phase shifted the 180°. When the signal is returned to the base, it has been shifted 180° by the action of RC network, making the circuit regenerative. The oscillation will be maintained if the loop gain (i.e. Avβ) is at least equal to unity. However, to start the oscillations, the loop gain must be greater than unity.
The phase shift occurs at only one frequency. At any other than the desired frequency, the capacitive reactance increases or decreases and causes an incorrect phase relationship. The, feedback becomes degenerative.
To find the resonant frequency fr. of an RC phase shift oscillator, use the following formula
Where n is the number of RC sections, R1 = R2 = R3 = R and C1 = C2 = C3 = C
A high gain transistor must be used with the three sections RC network because the losses in the network are high. Using more than three RC sections actually reduces the overall signal loss within the network. This is because additional RC sections reduce the phase shift necessary for each section, and the toss for each section is lowered as the phase shift is reduced. In addition, an oscillator that uses four or more RC network this has more stability than one that uses three RC networks. The phase shift oscillators can be used to produced very low frequencies and provides good frequency stability. They have one drawback i.e. when they are used to have a variable frequency circuit; it is difficult to adjust equally the capacitor values of the phase shift network simultaneously.
Wein Bridge Oscillator
An oscillator circuit, which is more useful for variable frequency operation, is the Wein-bridge oscillator. In such a case second stage of the amplifier is used for producing another 180o phase shift in addition to the phase shift of 180o produced by the first stage. Thus there is a total phase shift of 360°, which is equal to 0o. A fraction of the output from the second stage is feedback to the input of the first stage without producing any further phase shift. The RC oscillator utilizing this principle is called as Wein-bridge oscillators.
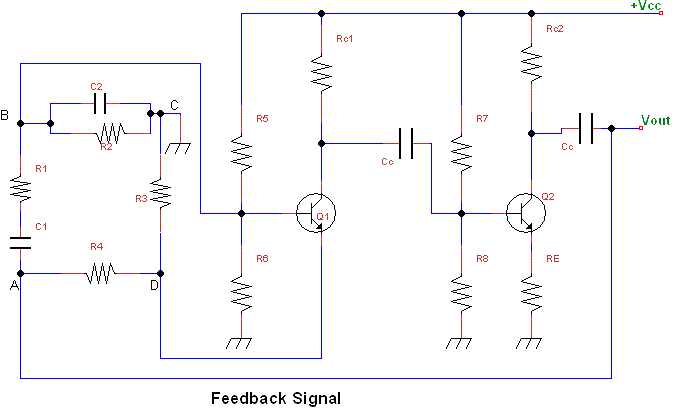
Figure shows the circuit of a Wein-bridge oscillator using transistors. The circuit consists of a two-stage RC coupled amplifier, which provide an approximately 360o or 0o phase-shift. So the feedback network has no need to induce any additional phase-shift. The feedback network consists of C1 - R1, C1 - R1 (called a lead-lag network) and C1 - R1 (cat voltage-divider). The lead-lag network provides a positive feedback to the input of the first stage and the voltage-divider provides the negative feedback to the emitter of Q1 transistor, it can be shown by a simple analysis that the frequency of oscillations for the wein-bridge oscillator is given by the relation,
And the ratio of resistor R3 to R4
R3/R4 = 2
Thus a ratio of R3 to R4 greater than 2 will provide a sufficient gain for the circuit to oscillate at the desired frequency.
