Ramp Generators
Voltage and current linear ramp generator find wide application in instrumentation and communication systems. Linear ramp generators are also known as sweep generators, from basic building blocks of cathode ray oscilloscope and analog to digital converters. Linear current ramp generator are extensively used in television deflection systems. This topic consider the circuits employed in the generation of voltage and current sweeps.
Ramp Generation Methods
Although there are a number of methods of ramp generation, yet the following are important from the topic point of view.
Exponential Charging
In this method a capacitor is charged through a resistor to a voltage which is small in comparison with the supply voltage.
Constant Current Charging
In this method a capacitor is charged linearly from a constraint current source.
Miller Integration
In this method a constant current is approximated by maintaining nearly constant voltage across a fixed resistor in series with a capacitor.
RC Ramp Generator
Figure 1 shows the basic circuit of RC ramp generator. This circuit requires a gating waveform Vi as shown in Figure 1(b). It may be obtained from a Monostable multivibrator (i.e. one shot) or an Astable multivibrator.
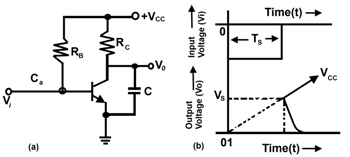
Initially the transistor is biased ON and operates in the saturation region. Thus when there is no input (i.e. Vi = 0 ), the output voltage is zero. Actually its value is equal to VCE (sat). When gating pulse i.e. a negative pulse is applied the transistor turns OFF. As a result of this, the capacitor voltage rises to a target value VCC with a time constant RCC. The charging curve ignoring VCE (sat) is given by the relation.
If t / RCC << 1, then above relation may be expanded into a power series in t / RCC. Then taking only the first term of the power series, the output voltage.
This equation represents an approximately linear waveform.
It may be observed that the transistor switch is OFF only for the gating time (TS). At the end of time TS, the capacitor discharges and the voltage is again zero.
Constant Current Ramp Generator
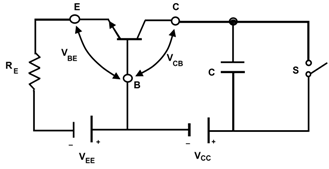
Figure 2 shows a circuit to generate a ramp using constant current from a common base transistor. We know that except for very small value of collector to base voltage, the collector current of a transistor in the common base configuration is very nearly constant, when the emitter current is held fixed. This characteristics may be used to generate a quite linear ramp by causing a constant current to flow into a capacitor. The value of emitter current is given by the relation.
IE = ( VEE - VEB ) / RE
If the emitter to base voltage VEB remains constant with time after the switch S is opened, then the collector current will be a constant whose normal value,
IC = hFB . IB = α IE
The draw back of constant current ramp circuit is that it makes the sweep rate as a function of temperature. Since the emitter base junction voltage VBE for a fixed current decreases by about 2 mv/co, therefore the ramp speed increases with the temperature.
UJT Relaxation Oscillator
The UJT relaxation as a relaxation oscillator is shown in Figure 3, generates a voltage waveform VB1(Figure 3), which can be applied as a triggering pulse to an SCR gate to turn on the SCR. When switch S is first closed, applying power to the circuit, capacitor C starts charging exponentially through R to the applied voltage V. The voltage across its the voltage VE applied to the emitter of UJT. When C has charged to the peak point voltage VP of the UJT, the UJT is turned on, decreasing greatly the effective resistance RB1 between the emitter and base 1. A sharp pulse of current IE (limited only be R1) flows from base 1 into the emitter, discharging C. When the voltage across C has dropped to approximately 2V, the UJT turns off and the cycle is repeated. The waveforms in figure 3 shows the saw-tooth voltage VE, generated by the charging of C and the output pulse VB1 developed across R1, VB1 is the pulse which will be applied to the gate of an SCR to trigger the SCR.
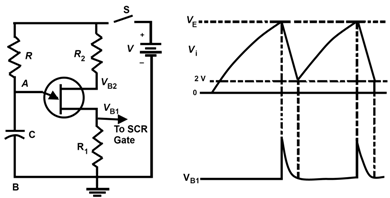
The frequency f of the relaxation oscillator depends on the time constant RC and the characteristics of the UJT. For values of R1 < 100KΩ, the period of oscillation T is given approximately by the equation.
T = 1 / f = RT CT 1Ƞ (1 / 1 - Ƞ)
The value of R is limited to the range 3000Ω to 3MΩ. The supply voltage V normally used lies in the range of 10 to 35 V and etc Ƞ is called intrinsic standoff ratio of injunction transistor ( i.e. ratio of RB1 and RBB)
Bootstrap Ramp Generator
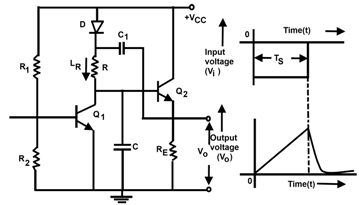
Figure 4 shows the bootstrap ramp generator. In such case the transistor Q1 acts as a switch and Q2 as an emitter follower i.e. a unity gain amplifier.
Suppose the transistor Q1 is ON and Q2 is OFF. Therefore the capacitor C1 is charged to VCC through the diode forward resistance RE. At this instant, the output voltage Vo is zero.
When negative pulse as shown in Figure 4 is applied to the base of transistor Q2 it turns OFF. Since transistor Q2 is an emitter follower, therefore the output voltage (Vo) is the same as the base voltage of transistor Q2. Thus as the transistor Q1 turns OFF, the capacitor C1 starts charging this capacitor C through resistor R. As a result of this , both the base voltage of Q2 and the output voltage begins to increase from zero. As the output voltage increases, the diode D becomes reverse biased. It is because of the fact that the output voltage is coupled through the capacitor C1 to the diode. Since the value of capacitor C1 is much larger than that of capacitor C, therefore the voltage across capacitor C1 practically remains constant. Thus the voltage drop across the resistor R also remains constant because of this, the current iR through the resistor also remains constant. This causes the voltage across the capacitor C (and hence the output voltage) to increase linearly with time.
Miller Integrator Ramp Generator
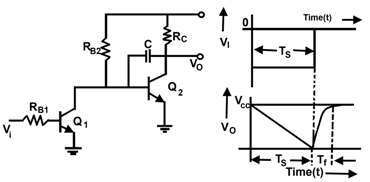
Figure 5 shows the miller integration ramp generator. It is also called Miller integrator. In such a case transistor Q1 acts as a switch and transistor Q2 is a common emitter amplifier i.e. a high gain amplifier.
Suppose that initially, the transistor Q1 is ON and Q2 is OFF. At this instant, the voltage across the capacitor and the output voltage is equal to VCC. Let us suppose that a pulse of negative polarity as shown in Figure 5(b) is applied at the base of the transistor Q1. As a result of this, the emitter-base junction of the transistor Q1 is reverse biased and it turns OFF. This causes the transistor Q2 to turn ON.
As the transistor Q2 conducts, the output voltage begins to decrease towards zero. Since the capacitor C is coupled to the base of transistor Q2 therefore the rate of decrease of the output voltage is controlled by the rate of discharge of capacitor C. The time constant of the discharge is RBC.
As the value of time constant is very large, therefore the discharge current remains constant. Hence a result of this, the rundown of the collector voltage is linear.
When the input pulse is removed the transistor Q1 turns ON and Q2 turns OFF. It will be interesting to know that as the transistor Q1 turns OFF, the capacitor C charges quickly through resistor RC to VCC with the time constant equal to RCC. The waveform of the generated ramp or the output voltage is shown in Figure 5(b). The Miller integrator provide an excellent ramp linearity as compared to the other ramp circuits.
