Testing Of Induction Motor
Like other machines induction motors are tested to get the necessary information to know parameters, losses, efficiency, speed, torque, current, P.f., etc. The following tests are made on induction motors:
- Direct test
- No-load test
- Blocked (or locked) rotor test
Direct or Load Test
Another machine like a generator, mechanically coupled with the shaft of the motor acts as a load. The load on the motor is changed by changing the electric load on the generator. The output of the generator and input of the motor are determined by means of various meters connected as shown in Figure 1.
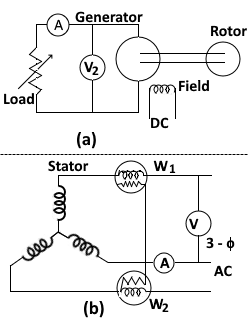
Figure 1: Direct or load test on 3 Phase induction motor
Let the generator is of DC type. Generator output = V2I2, where V2, I2 are output voltage and current:
Efficiency of generator, ηg = output of generator / Input of generator = V2I2 / input of generator
or
Input of generator = V2I2 / ηg
But input of generator = output of motor = V2I2 / ηg
The efficiency of the motor, ηm = output of motor / Input of motor = (V2I2/ ηg) / W1 + W2 where W1 + W2 = input power to the motor.
The direct test has the disadvantage of large consumption of power during testing, Also the availability of a load connected to the motor is necessary.
Indirect Or No-Load Test
The no-load test of an induction motor determines the friction and windage losses and the magnetization current. The no-load test is carried out with different values of applied voltage. The power input is measured by two wattmeters, no-load current "Io" by ammeter, and the input voltage "V" by voltmeter which are included in the circuit shown in Figure 2(a). The readings of the total power input "Wo", "Io" and voltage "V" are plotted as shown in Figure 2(b). If we extend the curve for "Wo" it cuts the vertical axis at point A. "OA" represents losses due to friction and windage. If we subtract the loss corresponding to "OA" from "Wo" then we get the no-load electrical and magnetic losses in the machine.
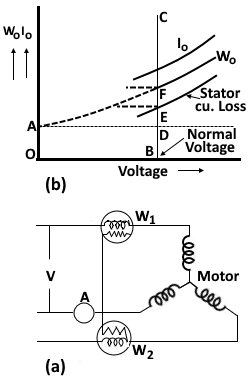
Figure 2: (a) No-Load Test (b) Curves obtained from No-Load test
"OB" represents normal voltage. Hence at normal voltage, the no-load input power "Wo" consists of:
(i) Small stator cu. Loss
(ii) Core loss
(iii) Loss due to friction and windageThese losses can be found from the curve by drawing a vertical line from B.
BD = loss due to friction and windage
DE = stator cu. Loss
EF = Core lossKnowing the core loss, Go, Bo, and Yo can be determined as
Go = Core loss / 3V2
Yo = Io/V
Bo = √( Yo2 – Go2)Input power factor angle can also be found from input power:
Wo = √3 VL Io Cos Øo
CosØo =√3 VL Io
Where
VL = Line voltage.Blocked Rotor Test
This test is also known as the locked-rotor or short-circuit test. This test is used to find:
- Short circuit current with normal voltage applied to the stator
- P.f. on short circuit
- Total Cu. Losses
- Equivalent circuit elements i.e., total leakage reactance "X01” referred to the stator, and total resistance "R01" referred to the stator.
In this test rotor is locked i.e. it is held stationary by some means. The rotor is short-circuited at slip rings if the motor has a wound rotor. Just as in the case of a short circuit test on a transformer, a reduced voltage (up to 20 percent of normal value) is applied to the stator terminals. This voltage is adjusted so that full load current flows in the stator. As here slip, equal to one, the equivalent circuit of the motor is exactly like a transformer having short-circuited secondary. The values of current, voltage, and power on the short circuit are measured by different meters connected to the circuit.
The following are found from this test:
Short circuit current ISN obtainable with normal voltage "V"
Let:
Zs = Short circuit impedance
Is = Short circuit current with voltage "Vs"
Short circuit current on normal voltage can be found as IsN = IsV / VsPower factor on the short circuit:
Ws =√3 VL ISL CosØs
CosØs = Ws / √3 VSL ISLwhere
Ws = short circuit input power
VSL = line voltage on short circuit
ISL = line current on short circuit.Cu. Loss.
Motor input on short circuits consists of mainly stator and rotor Cu. Losses and core losses:
Ws = Ccu + WCL
where Wcu = Total copper losses
WCL = Core losses
Or
Wcu = Ws - WCLR01, X01, Z01,
From an equivalent circuit diagram of the induction motor
Z01 = Vs/Is
And from total Cu. Losses
Wcu = 3Is2 R01
Or
R01 = Wcu/3Is2
X01 = Root (Z012 – R012)In the case of the squirrel cage rotor, R1 is determined as usual and after allowing for Skin effect is subtracted from R01 to give the effective rotor resistance R2 as referred to the stator.
R2 = R01 - R1
