Torque
The torque is defined as the turning or twisting moment of a force about an axis. The torque "T" produced by a force "F" acting on a body moving in a circle of radius "r", (Figure 1) is:
T = Fxr
If "F" is in Newton and "r" is in meter then unit of torque is Newton-meter (N-m).
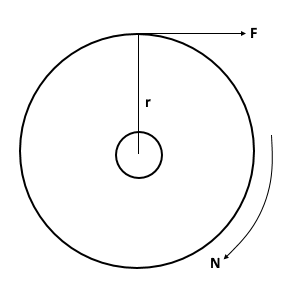
Figure 1
Work done by this force in one revolution = Force x distance
= F x 2 Δr Jouls
Let
N = revolution per seconds.
P = Power developed.
Power developed = F x 2 ΔrN Joules/second.
P = Fxrx2 ΔN
P = T x 2 ΔN
T = P / 2 ΔN
Let w = angular speed = 2 ΔN
T = P / ω --- (1)
In case of induction motor, the power developed = E1I2 CosØ2
where
E1 = stator induced e.m.f.
I2 = rotor current
CosØ2 = rotor power factor angle.
Putting this value in equation (1):
Torque, T = E1I2 CosØ2 / 2 ΔN
T α E1I2 CosØ2
As 1 / 2ΔN is a constant factor = K
T = K E1I2 Cos Ø2 ---- (2)
Also E1 α Ø
where Ø = flux per stator pole so we can write:
T = K1 Ø I2 Cos Ø2
where K1 = another constant.
STARTING TORQUE (Ts)
The torque developed by the motor at the instant of starting is called starting torque.
Let:
E1 = rotor e.m.f. per phase at stands till (i.e. at starting).
R2 = Rotor resistance per phase
X2 = rotor reactance per phase at standstill
Z2 = √(R22 + X2) = rotor impedance per phase at standstill
Then rotor current, I2 = E2/Z2 = R2/√(R22 + X22)
Power factor, Cos Ø2 = R2/Z2 = R2 / √(R22 + X22)
From equation(2)
Starting torque, Ts = K1 E1 I2 Cos Ø2
Putting values of I2 and Cos Ø2 we get:
Ts = K1E1(E1/√(R22 + X22)) ( R2 / √(R22 + X22)
Ts = ((K1E12 R2)/ (R22 + X22)) ------(3)
If supply voltage “V” is constant, then flux “Ø” and “E1” both are constant:
Ts = (K1E12) ( R2 / √(R22 + X22))
Ts = K2 (R2 / (R22 + X22)) -----(4)
Ts = K2 (R22 / Z22)
where K2 = K1E12
From the above equation it is clear that the value of starting torque can be increased by increasing the rotor resistance.
In case of squirrel cage rotor, the resistance of rotor is fixed and small as compared to its reactance. Hence starting torque of such motors are very poor. Such motors are not useful where the motor has to start against heavy loads.
The starting torque can be increased by adding extra resistances in the rotor circuit of slip ring motor at the start. Hence slip ring motors are used where the motor has to start against heavy loads.
CONDITION FOR MAXIMUM STARTING TORQUE
The condition for maximum starting torque can be found by differentiating torque equation (4) w.r. to "R2" and making it equal to zero:
The starting torque will be maximum when the rotor resistance per phase equals to the rotor reactance per phase.
RUNNING TORQUE (Tr)
When rotor starts running, the relative speed between the rotor and the rotating stator field decreases. Hence, rotor e.m.f. which is directly proportional to relative speed is also decreased. Hence the induced e.m.f. becomes slip times the induced e.m.f. at standstill.
Therefore, under running condition, Er = SE2.
Also frequency of induced e.m.f. becomes fr = sf so reactance under running condition becomes Xr = SX2 :
From equation (2).
Under running condition Torque, Tr =K1 Er Ir Cos Ø2
where:
CONDITION FOR MAXIMUM RUNNING TORQUE
To find the maximum running torque, here also differentiate the above equation w.r. to R2 and make it equal to zero, it results:
R2 = SX2
Hence torque under running condition is maximum at that value of slip "S" which makes rotor reactance perphase equal to rotor reactance per phase.
PULLOUT TORQUE
The running torque becomes maximum at the value of slip which makes rotor reactance per phase equal to rotor resistance per phase. This slip is called slip at maximum torque and this torque is called maximum or pullout torque or breakdown torque or stalling torque.
At pullout torque R2 = SX2 or S = R2/X2 putting this value in equation (5) of running torque:
The value of K3 can be proved to be equal to "3 / 2ΔNs ". From the above equation it is found that at "slip", maximum torque can be obtained by varying rotor resistance till it becomes equal to rotor reactance.
RELATION BETWEEN TORQUE AND SLIP
A family of torque/slip curves is shown in fig. 3.17 for a range of S = 0 to S = 1 with rotor resistance as parameter. We have seen that:
T = K3 ( SE2R2 / (R22+ (SX2))2
It is clear that when S = 0, T = 0, the curve then starts from point "0".
At normal speeds, close to synchronism, the term "SX2" is small and hence negligible w.r. to "R2"
T α S/R2
Or T α S if R2 is constant.
Hence for small values of S, the torque/slip curve is approximately a straight line. As slip increases (for increasing load on motor) the torque also increases and becomes maximum when S = R2/X2. This torque, as discussed above is called pullout or maximum torque. As the slip further increases (i.e. motor speed falls) with further increase in motor load, then R2 becomes negligible as compared to SX2. Therefore, for large values of slip:
T α S /(SX2)2 α 1/S
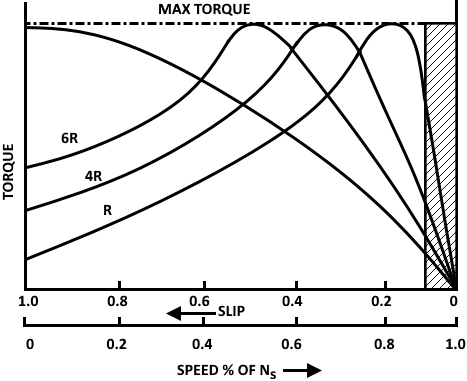
Figure 2: Torque / Slip Curves
We see that beyond the point of maximum torque, any further increase motor load results in decrease of torque developed by the motor. The result is that motor slows down and eventually stops. Therefore, stable operation of motor lies between the values of S = 0 and that value of "S" which is corresponding to maximum torque.
