Half Wave Rectifier One Plus Rectifier

Rectification is the process of converting alternating current or voltage into direct current or voltage. An uncontrolled rectifier uses only diodes as the rectifying elements. The DC output voltage is fixed in magnitude by the amplitude or the AC supply voltage. However, the DC output is not pure it contains significant AC components called ripple. To eliminate this ripple, a filter is inserted after the rectifier.

With Resistive Load

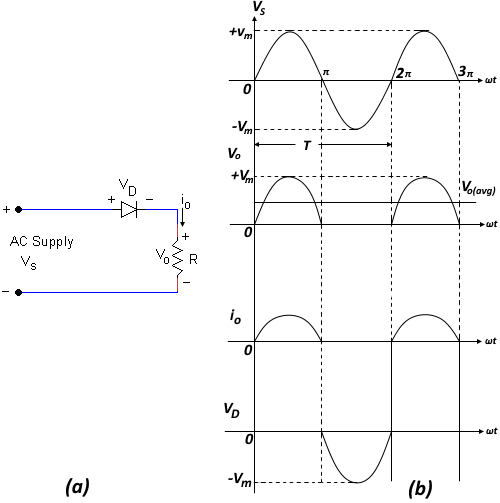
A simple half-wave rectifier circuit with resistive load is shown in Figure 1(a). The source voltage is a sine wave with a maximum value V_m and period T. During the positive half-cycle. When the voltage at the anode is positive with respect to the cathode, the diode turns on. This allows current through the load resistor R. Thus, the load voltage (V_o) follows the positive half sine wave. During the negative half-cycle, the voltage at the anode becomes negative with respect to the cathode and the diode turns off. Then no current flows through R. The output voltage (V_O) is shown in Figure 1(b), which also shows the load current.

The half wave rectifier thus changes AC power to DC. The output voltage is pulsating DC containing a large ripple. Therefore, one pulse circuits have limited practical value for high power applications.

The quantities of interest in this circuit are average or DC load voltage and load current.

Average load voltage is given by:

= V_m / π = 0.318 V_m

Where

V_S = the RMS value of supply voltage

V_m = the maximum value of supply voltage

The current waveform has the same shape as the voltage waveform, so a relation similar to equation 1 holds for the average load current.

I_C(avg) = I_m / π --------------------------------eq. 2

= 0.318 I_m

Where I_m = V_m / R

The root mean square (RMS) current is given by:

I_RMS = I_m / 2 ----------------------------eq. 3

The result in equation 3 is characteristic of the half wave circuit waveform.

.

The waveform of the diode voltage (Figure 1(b)) shows that the diode must be able to withstand a reverse voltage that is equal to the peak source voltage. This voltage is used to select the proper diode in a given circuit. The PIV (or PRV) rating for the diode is therefore given by:

PIV rating ≥ V_m

The purpose of a rectifier is to convert AC power into DC power. Since we are assuming ideal devices, with no power has in the rectifier, the net power flow at the AC input terminal averaged over a full cycle must equal the DC power output. The DC (average) power output to the load is given by:

P_O(avg) = V_O(avg) x I_O(avg)

= V_m / π x I_m / π

= (V_m x V_m) / (π² x R)

= V²_m / (π² x R)

The AC power input is given by:

P_AC = V_RMS x I_RMS

V_RMS for a period from 0 to π (half-cycle) is V_m / 2. Therefore,

P_AC = (V_m / 2) x (I_m / 2)

= (V_m X V_m) / (4 X R) = V²_m / 4R

The rectifier efficiency is defined as the ratio of DC output power to AC input power:

η = P_O(avg) / P_AC

The form factor is a measure of the goodness of the shape of the output voltage. Ideally, the DC output voltage of a rectifier should be constant. In practice, rectifiers provide outputs that are incomplete sine waves. The form factor is defined as the ratio of the RMS output voltage to the average value of output voltage.

Form factor (FF) = V_ORMS / V_O(avg)

The ideal value of FF is unity. FF is unity if the output voltage is a constant DC value, for which V_ORMS = V_O(avg).

The output voltage of a rectifier contains both DC and AC (ripple) components. The frequency and magnitude of the ripple voltage is an important factor in the choice of rectifiers. The higher the frequency and the smaller the magnitude of the ripple, the easier it is to filter the ripple to within acceptable limits. The pulse number is the ratio of the fundamental ripple frequency of the DC voltage to the frequency of the AC supply voltage.

Pulse number = fundamental ripple frequency / AC source frequency. The ripple factor is the ratio of the RMS value of the AC components to the DC component

Ripple factor = I_oAC / I_oDC

Ideally the ripple factor should be zero. The ripple factor can be determined first finding the power dissipated in the load resistor R

P_L = I²_RMS R = I²_DC R + I²_AC R

or

I²_AC = I²_RMS – I²_DC

I²_AC / I²_DC = (I²_RMS / I²_DC) – (I²_DC / I²_DC)

RF² = (I²_RMS / I²_DC) – 1

With an Inductive load

The half wave circuit with an inductive (RL) load, which is the practical case, is shown in Figure 2(a). Let us analyze the operation of this circuit.

1. As in the case of a resistive load, the diode turns on when its anode becomes positive with respect to the cathode. The voltage across the load is therefore the same as the positive half-cycle of the AC source.

2. During this time, energy is transferred from the AC source and is stored in the magnetic field surrounding the inductor.
3. The current through an inductor cannot change instantaneously. Therefore, the current increases gradually until it reaches its maximum value. Note that the current does not reach its peak when the voltage is at its maximum. This is consistent with the fact that the current through and inductor lags the voltage.
4. When the source voltage decreases, the current through an inductor lags the voltage becoming zero when all the energy stored by the inductor is released to the circuit. The load current therefore exists for a little more than half the entire period.
5. At the same time the collapsing magnetic field links with the inductor and induces a voltage that opposes the decrease in the applied voltage.
6. As soon as the current is zero, the diode is reverse biased. The diode then remains off for the rest of the negative cycle. Figure 2(b) shows the waveforms.

During the interval from 0 to π/2, the source voltage V_S increases from zero to its positive maximum, while the voltage induced across the inductor V_L opposes the change of current through the load. In the time interval π/2 to π, the source voltage decreases from its positive maximum value to zero. At the same time, the induced voltage has reversed polarity and opposes the decrease in current; that is, it now aids the diode forward current.

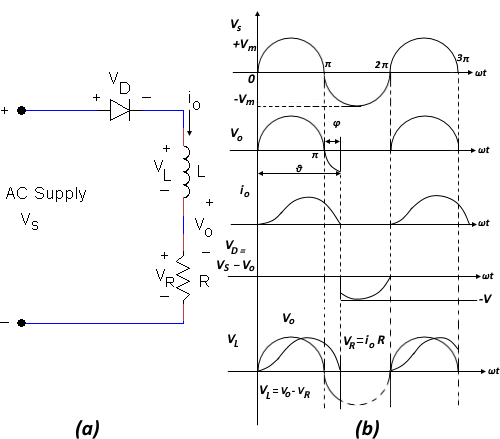
At π, the source voltage reverses and starts to increase to its negative maximum value. However, the voltage induced across the inductor is still positive and will sustain forward conduction of the diode until the induced voltage decreases to zero, at which point the diode blocks. Note that although the diode is reverse biased, there is a current flow through the diode until the angle θ = π + φ is reached. This is the result of the energy stored in the magnetic field being returned to the source.

.

The waveform of voltage across the resistor is the same as the waveform of i_O (V_R = i_OR). The difference between V_R and V_O. is the voltage across the inductor (see Figure 2(b)).

If we increase the load inductance L, the diode will conduct current for more time during the cycle.

If we assume L to be infinite, the current that flows through the diode would be completely smooth and therefore continuous. In this situation, the diode would be on for the full cycle, the voltage across the diode would be zero, and the values of V_S and V_D would be equal. The circuit would no longer rectify, so the current would be alternating. This is not possible; therefore the output current must be zero for some duration that is less than half a cycle. The average output voltage therefore depends on the relative inductance and resistance of the load. The waveforms shown in Figure 2(b) are drawn for the case in which the average output voltage is not zero and the current is therefore not continuous.

The average value of the load voltage is given by:

V_O(avg) = (V_m/ 2π)(1 – cos θ)

Where θ = π + φ is the conduction angle, (φ depends on the values of L and R)

It should be clear from the above that as:

Φ approaches 180^O_,V_O(avg) approaches zero

Θ approaches 360^O, V_O(avg) approaches zero

In other words, the inductive load reduces the average load voltage.

Note that if θ = 180^O, then V_O(avg) = V_m / π (eq. 1)

For high power applications, one pulse circuits have limited practical use due to their low output voltage and the large ripple that is contained in the DC output voltage.

With an Inductive Load and a Freewheeling Diode (FWD)

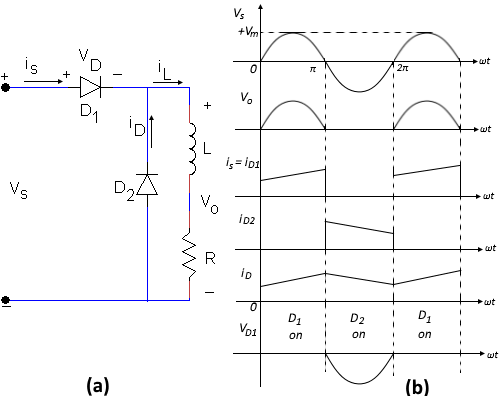
The circuit in Figure 2 can be modified to produce the circuit shown in Figure 3. used in low power applications. It is still considered a halfwave rectifier, although the load current can flow for the entire cycle.

The second diode D₂, which is added in parallel with the load, is known as a freewheeling diode (FWD). this diode prevents negative voltage from appearing across the load, and as a result, it increases the average output voltage (V_O(avg)) across the load as well as the average current I_O(avg). During the negative half-cycle of the supply voltage, the FWD conducts and provides an alternate path for the load current. During this interval of FWD conduction, the main diode D₁ is reverse biased and stops conducting, and thus the source current is zero for this half period. The FWD helps to prevent the load current from ever going to zero and thus reduces the ripple.

The load voltage waveform is the same as in the halfwave circuit with a resistive load. The average load voltage is similarly V_m / π, as given by eq. 1.

The voltage and current waveform shown in this figure assume a large load inductive. The larger the load inductance, the smoother the load current becomes.