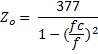Waveguide - Group Velocity, Phase Velocity, Cut off Frequency & Impedance

Waveguides are transmission structures that guide electromagnetic waves along a path. They are commonly used for radio frequency signals, microwaves, optics, and more. An important parameter for waveguides is the group velocity, which refers to the velocity at which the overall shape of the wave's amplitudes propagates through the guide.

Group Velocity

The group velocity vg describes the velocity at which the envelope of a wave's amplitudes moves through a medium. It is determined by the dispersion relation of the waveguide, which relates to the frequency and wavelength. Group velocity is defined by the equation:

vg = dω/dk

Where ω is the angular frequency and k is the wavenumber. For typical waveguides, the group velocity is less than the phase velocity vp.

Explaining Group Delay

As a wave travels through a guide, its phase velocity vp transports the phase of its harmonic components. But the propagation of the entire waveform shape and modulation is governed by vg. The difference between these velocities causes dispersion - a delay between phase and group transit times called group delay:

τg = vp - vg

This group delay phenomenon is key to understanding dispersion performance.

Relating Group Velocity to Guide Properties

For common rectangular waveguide modes, vg can be derived from the guide's dimensions and the signal wavelength. Cutoff frequency, operating frequency, and dielectric properties alter these velocities for a given mode. Group velocity helps characterize dispersion and power flow.

Phase Velocity

Phase velocity is a key parameter that characterizes wave propagation in waveguides and other transmission media. It describes the speed at which the phase of individual frequency components of a wave travels through a guide.

Defining Phase Velocity

Phase velocity (vp) is defined as the rate at which the phase of a sinusoidal component of the wave propagates. For a harmonic wave:

vp = ω/k

Where ω is the angular frequency and k is the wavenumber. The wavenumber is related to wavelength λ by:

k = 2π/λ

Thus, phase velocity can also be expressed as:

vp = λf

Where λ is the wavelength and f is the frequency.

Relating Phase Velocity to Waveguide Properties

For common rectangular waveguide modes:

• vp depends on the guide dimensions and dielectric
• vp is greater than the speed of light in the dielectric
• vp is independent of frequency

For other types of guides, the dispersion relation will determine how vp varies with frequency.

The Importance of Phase Velocity

Phase velocity indicates the speed of individual frequency components. But the propagation of the entire waveform envelope relies on group velocity. The difference between vp and group velocity vg leads to dispersion effects. Phase velocity provides insights into phase shifting and energy transport along the guide.

Cut Off Frequency

It is the frequency that cannot be propagated through the waveguide. Its symbol is fc.

Formulas

Fc = c/2a

Here fc stands for cut-off frequency C stands for velocity of Electromagnetic waves in free space. Which is 3 x 10⁸ m/s. Stands for the broad dimension of the waveguide?

λg = wavelength of the electromagnetic waves inside the waveguide.
f   = frequency in free space
c   = velocity of electromagnetic wave in free space
fc = cut off frequency

The broad dimension of the waveguide is 5cm. find its cut-off frequency.

Fc = c/2a
Fc = 3x10¹⁰ cm / 2 x 5 cm
Fc = 3 x 10⁹ Hz
Fc = 300 MHz
F = 3 GHz

Impedance (Zo) of waveguide

The characteristics impedance (Zo) is known as the impedance infinity of a long waveguide. If the load which is connected with the waveguide is terminated with its characteristic impedance, then the whole energy is consumed by the load and no reflected energy is transferred back toward the source.

Here

Zo = Characteristic impedance of the waveguide
λg = waveguide length (the wavelength of the frequency traveling through the waveguide)
λo = Wave length of the operating frequency

Here

fc = cut-off frequency of the waveguide
f = operating frequency in free space